向量索引技术

向量嵌入只是从图像、文本和音频转换而来的数值表示。简单来说，针对每个项目创建一个单独的数学向量，捕捉该项目的语义或特征。这些向量嵌入更容易被计算系统理解，并与机器学习模型兼容，以理解不同项目之间的关系和相似性。

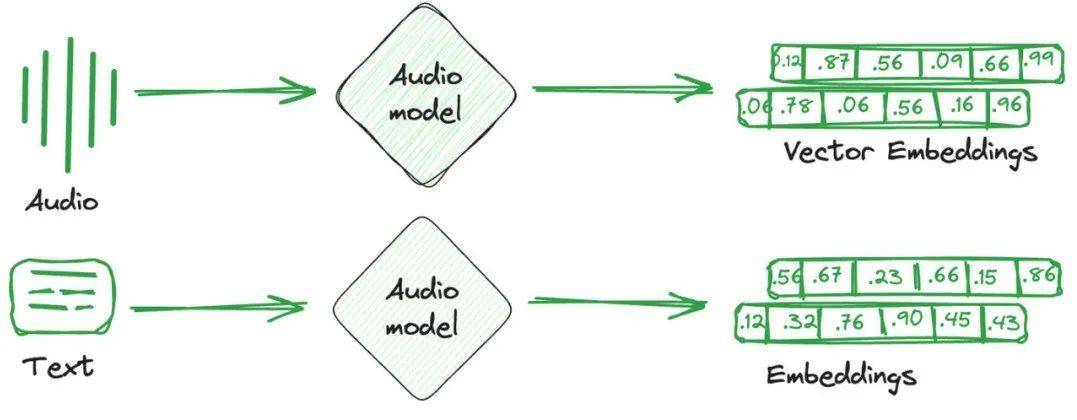
用于存储这些嵌入向量的数据库称为向量数据库。这些数据库利用嵌入的数学属性，将相似的项目存储在一起。使用不同的技术来将相似的向量存储在一起，将不相似的向量分开。这些就是向量索引技术。

什么是特征向量

向量是一种将实体和应用代数化的表示。向量将实体间的关系抽象成向量空间中的距离，距离的远近代表相似程度。例如：身高、年龄、性别、地域等。

除了图像、文本和音频，理论上所有包含文本在内的任意数据都可以向量化，引用一句网上的热门词就是「万物皆可 Embedding」。

什么是向量索引

向量索引通过将数据表示为向量，并构建高效的索引结构，可以实现快速的相似性搜索和匹配，提高数据检索和匹配的效率。

什么是距离计算

向量检索的过程是计算向量之间的相似度，最后返回相似度较高的 TopK 向量返回，而向量相似度计算有多种方式，不同的计算方式也适用于不同的检索场景。

对于浮点型向量和二值型向量有着不同的距离计算方式。

在实际的应用工程应用场景中，绝大多数使用的浮点型计算，故下面核心介绍浮点型计算距离。

内积距离

内积距离计算的是两个向量在方向上的差异，夹角越小越相似，因此内积值越大越相似。

两条向量内积距离的计算公式为：

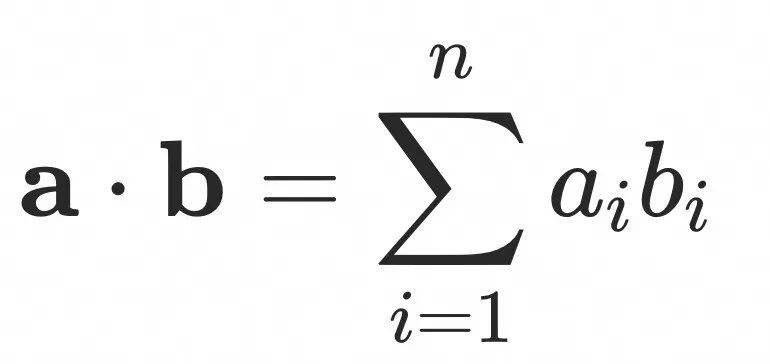
内积更适合计算向量的方向而不是大小，通常用于推荐场景。

内积在几何意义上是计算一条向量在另一条向量上的垂直投影长度。

欧式距离

欧氏距离计算的是两点之间最短的直线距离，距离值越小越相似。

欧氏距离的计算公式为：

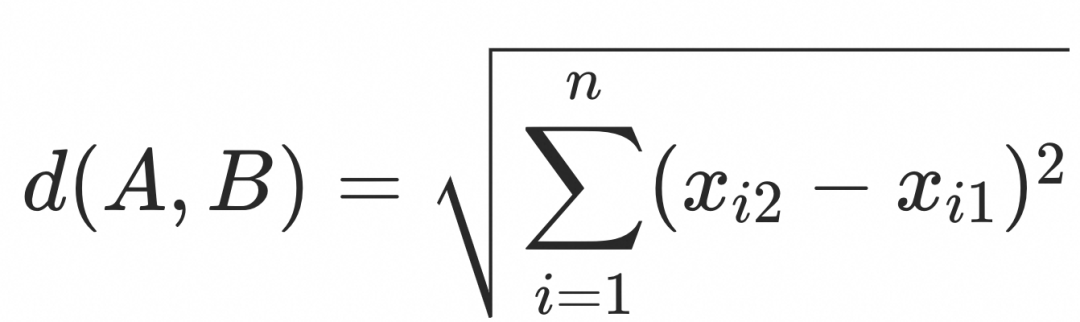
欧氏距离是最常用的距离计算方式之一，应用广泛，适合数据完整，数据量纲统一的场景。

欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异。

余弦距离

余弦距离计算的是两个向量之间的夹角余弦值，夹角越小越相似，因此余弦相似度值越大越相似。

余弦距离的计算公式为：

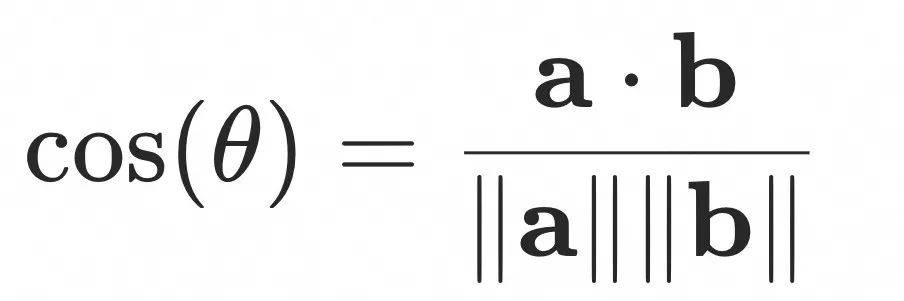
余弦距离和内积距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题。

基础算法

上述介绍了向量检索的计算相似度方式，接下去就要研究如何加快检索速度。向量检索的本质是近似近邻搜索（ANNS），尽可能减小查询向量的搜索范围，从而提高查询速度，目前业界的近邻搜索算法主要分为基于树、图、量化和哈希四类。考虑到本文核心讲解 RAG 中的工程技术，故本文对此不做过多介绍，有兴趣的读取可以自行深入了解学习。

稠密 & 稀疏向量检索模型

稠密向量检索模型和稀疏向量检索模型是信息检索领域的两种主要方法，主要用于从海量数据中快速查找相关信息。两者的核心区别在于向量表示和搜索方式。

稠密向量检索模型

定义：稠密向量检索模型使用神经网络等深度学习技术，将文档和查询转换为高维稠密向量。每个向量的维度都包含实数值，并且通常维度的数量较少（如几百到几千维）。

特点：

向量表示：每个数据点被表示为一个长度较小、但密集的数值向量。

搜索方式：通过计算向量间的距离（如余弦相似度、欧氏距离）来进行匹配和检索。

优点：能够捕捉复杂的语义关系，表现出色的泛化能力，适合语义相似度计算。

缺点：模型训练需要大量数据和计算资源；搜索阶段需要进行高效的近似最近邻搜索。

稀疏向量检索模型

定义：稀疏向量检索模型通常基于传统的语言模型（如 TF-IDF）和袋装词模型，将文档表示为高维稀疏向量，每个维度对应一个独立的词项。

特点：

向量表示：通用的是利用词项的频率来表示向量，向量的维度非常高（通常和整个词汇表的大小一样），但其中大部分维度的值为零。

搜索方式：通过倒排索引等结构来快速检索和匹配文档。

优点：成熟稳定，解释性强，索引和检索效率高。

缺点：难以捕捉词语间的复杂语义关系，可能对词汇的同义关系不敏感。

区别总结

表示方式：稠密模型使用低维稠密向量，稀疏模型使用高维稀疏向量。

语义能力：稠密模型更擅长捕捉深层语义，稀疏模型在简单文本匹配上更有效。

计算资源：稠密模型通常需要更多计算资源用于训练和检索，稀疏模型则通常拥有更快速的索引和检索过程。

应用场景：稠密模型适合需要深层语义理解的任务，稀疏模型则适用于快速精确匹配场景。