电子电荷密度

无论是电荷密度差异还是电荷布居分析，其根源都是体系的电子电荷密度。

但是电子电荷密度是如何获得的呢？

我们知道，在第一性原理计算中，需要求解体系的电子薛定谔方程。该方程的解可得到基态能量E和波函数ψ(r)系统中的电子。

该系统的电子概率密度由波函数的平方给出：

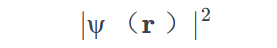
一个区域内的电子电荷密度与该区域电子存在的概率密度成正比。因此，该系统的电子电荷密度为：

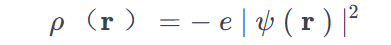
e是电子电荷的绝对值。当我们将系统的单位电荷定义为e=1，电子电荷密度变为：

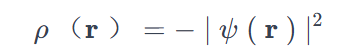
求解薛定谔方程得到的电子电荷密度与系统的实际电荷密度有什么关系

首先，显然在计算电子电荷密度时不考虑带正电的原子核。其次，在求解薛定谔方程时，我们通常只求解外层价电子，而将内层电子视为核心电子，不参与计算。因此，计算出的电荷密度与系统的实际电荷密度存在差异。值得庆幸的是，由原子核和核心电子组成的原子核在化学反应过程中变化很小，对分析电子转移的贡献可以忽略不计。因此，计算价电子通常可以很好地表征化学反应过程中的电子转移行为。

电荷密度差

知道了电子电荷密度，我们首先来讨论一下电荷密度差。

所谓电荷密度差，是指体系经过吸附、置换等操作后，其电荷密度与操作前的电荷密度之差。

为什么要进行吸附和置换呢?因为在这些操作中，原子核的位置可以保持不变。

例如，吸附涉及从吸附体系的电荷密度中减去吸附前表面和分子（在其吸附后几何结构中）的电荷密度。即使在优化过程中会发生结构变化，对于电荷密度差异计算，也会使用吸附后几何结构进行单点计算，以确保几何结构保持不变。

同样的原理也适用于置换，即一个原子被另一个原子取代，同时所有原子位置保持不变。在这种情况下，原子核的位置保持不变，核心电子的分布也不会改变。因此，电荷分布的变化等于价电子分布的变化。

电荷密度差二维热图和三维等值面

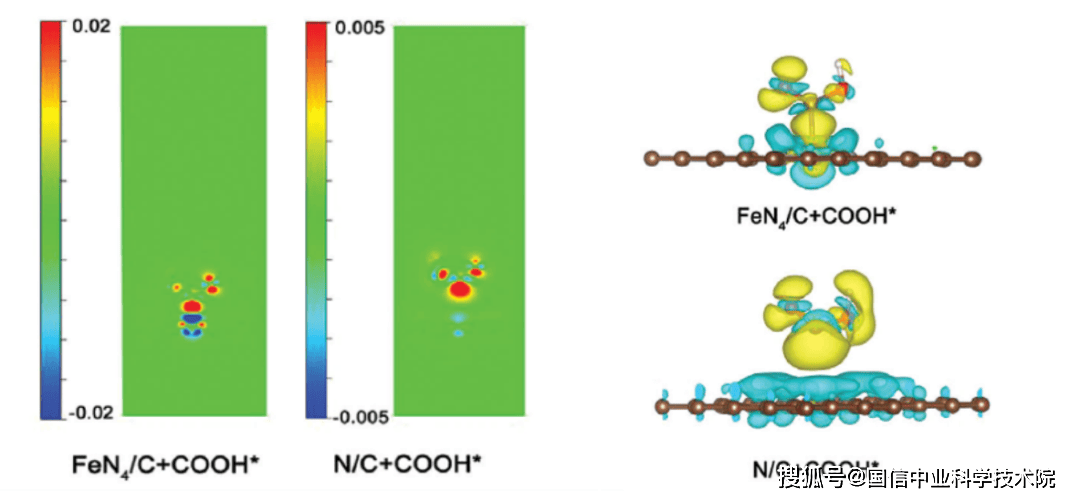图 1：电荷密度差 2D 热图和 3D 等值面

电荷密度差可以通过不同方式可视化：

• 在特定平面上以彩色二维热图形式呈现
• 以三维等值面形式呈现

如图 1 所示，这些是同一两个系统的电荷密度差异图（2D 和 3D）。

• 在左侧热图中，红色表示电荷积累区域，蓝色表示电荷耗尽区域。
• 在右侧的 3D 等值面图中，黄色表示电荷增加，浅蓝色表示电荷减少。

这些图谱常用于讨论体系中的键合情况。例如，图1展示了COOH在FeN₄/C和N/C上吸附的电荷密度差异图。从左侧热图可以看出，两个体系都表现出吸附物和表面之间的电荷积累。然而，色标有所不同：左图中最高电荷密度为0.02，而右图中最高电荷密度为0.005。这表明在FeN₄/C体系中，更多的电子积累在键合区域，从而导致更强的吸附。

巴德电荷布局

虽然电荷密度差异图可以直观地显示化学过程中的电子转移，但它们是定性的。当电荷增加和减少的区域具有复杂的几何形状且相互交织时，很难从图像中提取有意义的结论。因此，有时使用定量方法来计算与每个原子相关的电子数量，这有助于分析化学过程中原子级的电荷转移。这些方法属于电荷布居分析。

电荷布居分析有很多种类型，例如 Bader 法、Mulliken 法、Löwdin 法、Hirshfeld 法等等。这些方法不仅能计算每个原子的电荷，还能计算原子轨道上的电子数。本文我们仅讨论 Bader 法电荷分析。

Bader电荷分析原理

Bader 电荷分析基于电荷密度中的零通量表面的概念。

原子之间的边界是如何定义的？

由于电子密度在原子核附近最高，因此它会随着与原子核距离的增加而减小。密度下降最快的方向是梯度方向。沿着这个方向移动会导致电子密度持续下降，直到到达受另一个原子影响更大的区域。跨越这个边界，虽然离原子A更远，但会靠近原子B，密度也会增加。在这个边界上，电荷密度梯度为零——这被称为零通量表面。

在Bader分析中，每个原子核周围被零通量表面包围的区域被定义为该原子的“域”。对该域内的电子密度进行积分，可以得出分配给该原子的电子数——这是Bader电荷分析的基础。

典型电荷分布

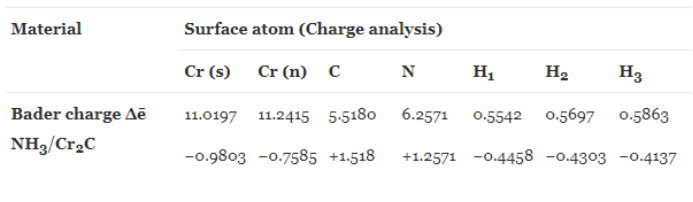图2.典型的电荷分布表

电荷分布结果通常以表格形式呈现。

• 有时他们会报告每个原子的价电子数（图 2 中的第一行）。
• 其他时候，他们会添加核电荷来报告总原子电荷（图 2 中的第二行）。

Bader电荷分析通常用于确定吸附过程中的电荷转移并解释吸附相互作用的强度。

• 如果发生显著的电荷转移，则表明表面和吸附物之间存在强烈的相互作用。
• 如果发生很少的电荷转移，相互作用可能会很弱。

然而后者也有例外。例如，O-O 或 N-N 键可能由于电负性相同而很强，导致净电荷转移很少。

因此，虽然大量电子转移通常表示强相互作用，但缺乏电荷转移并不一定意味着弱键合。

结论

本文介绍了电荷密度差和Bader电荷分析的概念。

两者都基于价电子的空间分布：

• 电荷密度差：定义为涉及固定核的过程之前和之后的电荷密度差。
• Bader 电荷分析：使用电荷密度的零通量表面定义与每个原子相关的电荷。

这两种方法均可用于分析过程期间的电子转移，从而推断化学相互作用的存在和强度。