01　题目呈现

真空中，电荷量均匀分布在半径为的球面上。在球面上取一极小面积，其电荷量为，。已知静电力常量为，求受到其它电荷对它的作用力。

02　积分解之

以球心为原点，指向点电荷方向为正方向定为轴正方向，如图所示。与轴夹角为处取微小角度，以轴为转轴旋转一圈，形成一条窄带，其面积用表示。由于对称性，这一条窄带对点电荷的作用力沿着轴正方向。

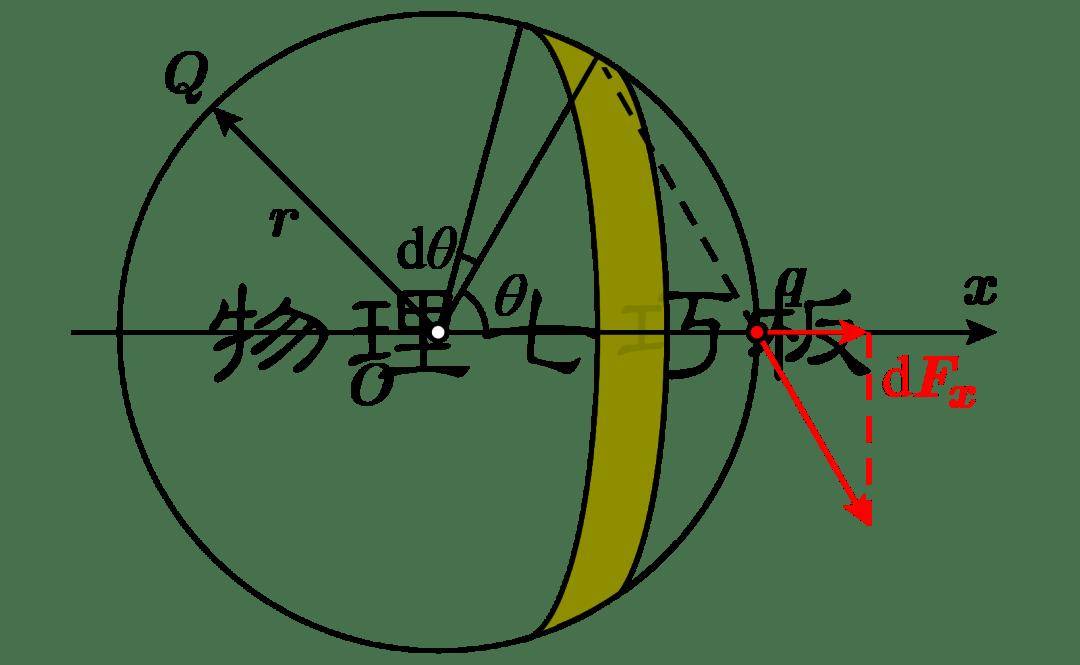
所对的弧长为

窄带的面积为

球面的电荷密度为

窄带所带的电荷量为

窄带对点电荷的作用力为

从，对积分，得到点电荷受到的力

03　补充说明

〔1〕积分上下限

由于点电荷所占面积极微小，所以积分的时候，不考虑其大小，直接从开始算起。被积函数与成正比，在处并没有趋于无穷大。因此可以忽略微小角度造成的积分结果不一致。

〔2〕若非微小面积

如果问题改为“单位面积球壳受到的静电力”，这时候就不能从开始积分了。如果不能积分，我们可以考虑一下程书的解法：

容易发现，这个结果和前面积分的结果是不矛盾的。

04　是不是

程书里面出现了一个很关键的词——单位面积。

〔1〕静电压强

该怎么理解这个“单位面积”好呢？咋一看，似乎它应该指的是“”，至少在国际单位制的前提下，我们会默认如此。

但这也只是咋一看罢了，毕竟球的表面积可能都不到“”。

正如不能说就真得需要走。

所以，“单位面积球壳受到的静电力”应该理解为“球壳受到的静电压强”。这里有一个已经成立的前提，即球壳的任何一处受到的静电力都和球壳垂直。用垂直于面的力除以面积，得到的自然是压强，所以我称之为静电压强。似乎也有些地方称之为静电应力。

〔2〕面积的形状

有人非要纠结面积指的是某一具体的球壳部分，于是他假设一块球冠来计算受力。这时候我就想问：如果取的一块面积，是一条窄带，而这条窄带正好位于“赤道”呢？那岂不是应该受力为零吗？

所以，我们还是要把“单位面积球壳受到的静电力”理解为“球壳受到的静电压强”比较好。

05　最后

如果不是微小面积的电荷，我并不确定怎么去求解。欢迎大家补充。

【闲篇：3I/ATLAS去哪里了？我这可恶的降临派】